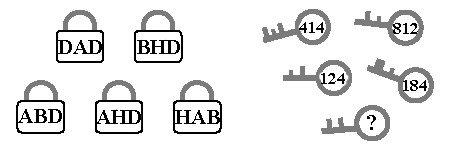1 . Quattro carte sono così allineate: .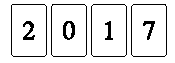
Quale di questi allineamenti non puoi ottenere scambiando di posto due sole carte?

(A) .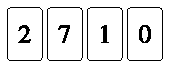
(B) .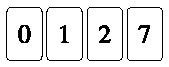
(C) .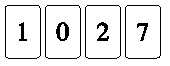
(D) .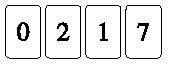
(E) .


2 . Una mosca ha 6 zampe, un ragno ne ha 8.
Tutti insieme, 3 mosche e 2 ragni hanno tante zampe quante ne hanno 9 canarini e ...
 
(A) 2 gatti.
(B) 3 gatti.
(C) 4 gatti.
(D) 5 gatti.
(E) 6 gatti.


3 . Alice ha 4 sagome di cartone di questa forma: .
Quale figura non può comporre con queste 4 sagome?

(A) .
(B) .
(C) .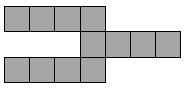
(D) .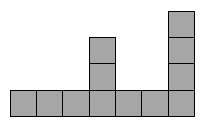
(E) .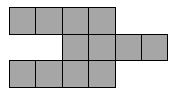


4 . Ti dico che 1111 x 1111 = 1234321.
Allora quanto vale 1111 x 3333?
(A) 3692963.
(B) 3698963.
(C) 3456543.
(D) 3579753.
(E) 3702963.


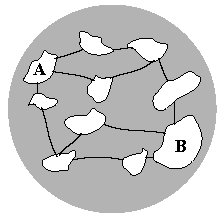
5 . In un arcipelago ci sono 10 isole e 12 ponti che le collegano come mostra la figura.


Al momento tutti i ponti sono aperti al trafico.
Qual è il minimo numero di ponti che occorre e basta chiudere per fermare il trafico tra l’isola A e l’isola B?
 
(A) 1.
(B) 2.
(C) 3.
(D) 4.
(E) 5.


6 . Giovanna ha 20 euro.
Ognuna delle sue quattro sorelle ha 10 euro.
Quanti sono gli euro che Giovanna deve dare a ciascuna delle sue sorelle perché ognuna delle cinque ragazze abbia la stessa quantità di denaro?
 
(A) 2.
(B) 4.
(C) 5.
(D) 8.
(E) 10.


7 . Maria ha lo stesso numero di fratelli e di sorelle; suo fratello Martino ha un numero di sorelle doppio del numero di fratelli.
Quanti figli ci sono nella loro famiglia?

(A) 4.
(B) 6.
(C) 7.
(D) 8.
(E) 9.


8 . Tre rinoceronti, Jane, Kate e Leila vanno in giro nella savana.
Jane cammina davanti, Leila cammina nel mezzo e Kate chiude la fila.
Jane pesa 500 kg più di Kate.
Kate pesa 1000 kg meno di Leila.
Se le dimensioni delle figure danno un’idea del peso degli animali, quale delle seguenti immagini mostra Jane, Kate and Leila nell’ordine corretto?

(A) .
(B) .
(C) .
(D) .
(E) .


9 . Nello stesso tempo in cui Piero risolve due quesiti della gara “Kangourou”, Nino riesce a
risolverne tre. A fine gara i due ragazzi hanno risolto in tutto 30 quesiti.
Quanti quesiti più di Piero ha risolto Nino?
 
(A) 5.
(B) 6.
(C) 7.
(D) 8.
(E) 9.


10 . Beppe ha piegato un foglio di carta, poi ha praticato un unico foro nella carta così piegata; infine ha aperto il foglio di carta. Vedi il risultato nella figura .


In quale modo Beppe aveva piegato il foglio di carta?

(A) .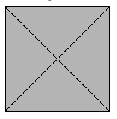
(B) .
(C) .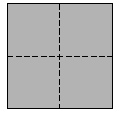
(D) .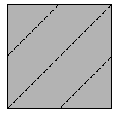
(E) .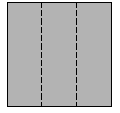


11 . Un dado speciale riporta un numero su ogni faccia.
Le somme dei numeri su facce opposte sono tutte uguali.
Cinque dei sei numeri sono 5, 6, 9, 11 e 14.
Quale è il numero sulla sesta faccia?
(A) 4.
(B) 7.
(C ) 8.
(D) 13.
(E) 15.


12 . Simone ha intenzione di suddividere un pezzo di spago in nove pezzi della stessa lunghezza e segna i punti in cui deve tagliarlo con un pennarello blu.
Barbara ha intenzione di suddividere lo stesso pezzo di spago in otto pezzi della stessa lunghezza e, a sua volta, segna i punti in cui deve tagliarlo con un pennarello rosso.
Arriva Carlo e taglia lo spago in tutti i punti in cui trova dei segni di pennarello.
Quanti pezzi di spago ottiene Carlo?
(A) 15.
(B) 16.
(C) 17.
(D) 18.
(E) 19.


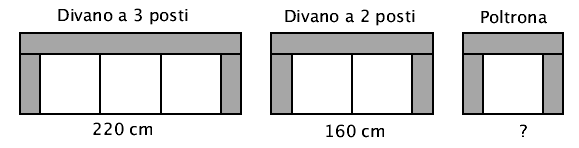
13 . Il magazzino Mobili Moderni vende poltrone e divani a 2 e 3 posti fatti degli stessi elementi modulari, come mostra la figura.


Inclusi i braccioli, la larghezza di un divano a due posti è 160 cm, quella di un divano a 3 posti è di 220 cm.
Inclusi i braccioli, quanti centimetri è larga la poltrona?
(A) 60.
(B) 80.
(C) 90.
(D) 100.
(E) 120.


14 . Milena ha fatto la costruzione che vedi a fianco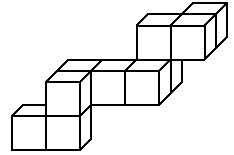 incollando dei cubetti di lato 1 dm e ora vuole metterla in una scatola a facce rettangolari.
Quali tra le seguenti sono le misure in dm della scatola più piccola che può usare?
(A) 3 × 4 × 4.
(B) 3 × 5 × 5.
(C) 3 × 4 × 5.
(D) 4 × 4 × 4.
(E) 4 × 4 × 5.


15 . Tom scrive tutti i numeri da 1 a 20 su una stessa riga e ottiene il numero di 31 cifre:
1234567891011121314151617181920

Poi cancella 24 delle 31 cifre in modo che il numero che rimane scritto (lasciando le cifre nell’ordine in cui si trovano) sia il più grande possibile.
Di che numero si tratta?
(A) 9671819.
(B) 9567892.
(C) 9781920.
(D) 9912345.
(E) 9818192.


16 . Ogni lucchetto può essere aperto da una sola delle cinque chiavi: quella il cui numero è
ottenuto sostituendo (nello stesso ordine) ogni lettera del lucchetto con una cifra, in modo che a lettere uguali, anche su lucchetti diversi, corrispondano cifre uguali.

Qual è il numero scritto sull’ultima chiave?
(A) 382   .
(B) 282.
(C) 284.
(D) 823.
(E) 824.


17 . Paolo è partito al lunedì per un’escursione di 5 giorni in montagna.
Ogni giorno dal lunedì al venerdì ha camminato 2 km in più del giorno precedente, percorrendo in tutto 70 km.
Quanti chilometri ha percorso giovedì?
(A) 12.
(B) 13.
(C) 14.
(D) 15.
(E) 16.


18 . Le lettere in figura 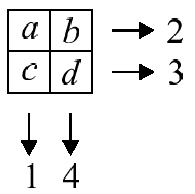rappresentano numeri interi maggiori o uguali a zero.
Sommando i numeri rappresentati in ciascuna riga e in ciascuna colonna si hanno i risultati mostrati in figura.
Quale delle seguenti affermazioni è vera?
(A) b è uguale a c.
(B) a è minore di d.
(C) a è maggiore di d.
(D) c è maggiore di b.
(E) Nessuna delle precedenti.


19 . Adriano ha una somma di denaro e 3 bacchette magiche:
• la bacchetta A aggiunge 1 euro alla somma;
• la bacchetta T toglie 1 euro alla somma;
• la bacchetta R raddoppia la somma.
Deve usarle tutte, ciascuna una sola volta. In quale ordine deve usarle per ottenere la maggior quantità possibile di denaro?
(A) R, A, T.
(B) A, T, R.
(C) R, T, A.
(D) A, R, T.
(E) T, A, R.


20 . Nell’immagine 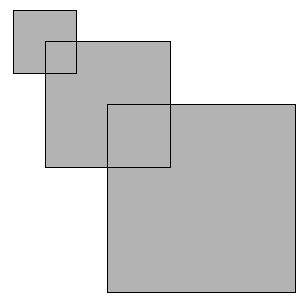vedi una figura formata sovrapponendo tre quadrati in modo che le parti sovrapposte siano quadrate.
Il primo ha lato lungo 2 cm, il secondo ha lato lungo 4 cm e un vertice nel centro del primo quadrato, l’ultimo ha lato lungo 6 cm e un vertice nel centro del secondo quadrato.
Quanti centimetri quadrati misura l’area della figura?
 
(A) 32.
(B) 51.
(C) 40.
(D) 56.
(E) 48.


21 . Raffaele ha delle barrette, ciascuna formata da 2 cubi grigi e uno bianco incollati insieme, come quella mostrata dalla figura .
Quale dei seguenti solidi può costruire con 9 di tali barrette?

(A) .
(B) .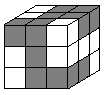
(C) .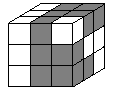
(D) .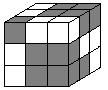
(E) .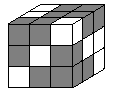


22 . Voglio inserire nelle cinque celle della figura a lato i numeri 1, 2, 3, 4, 5, seguendo le seguenti regole:
• se un numero si trova sotto un altro numero deve essere più grande di questo;
• se un numero è a destra di un altro numero, deve essere più grande di questo.
In quanti modi diversi posso farlo?
(A) 3.
(B) 4.
(C) 5.
(D) 6.
(E) 8.


23 . Nel primo triangolo a sinistra 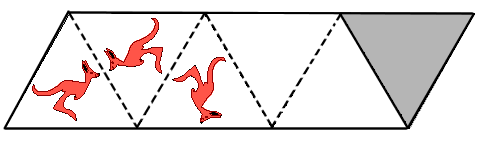è stato disegnato un canguro. Il canguro nel secondo triangolo è il simmetrico del primo rispetto al lato comune al primo e al secondo triangolo.
Il canguro nel terzo triangolo è simmetrico del secondo rispetto al lato comune al secondo e al terzo triangolo.
Se si procede allo stesso modo, quale delle seguenti è l’immagine che si vedrà nel triangolo grigio?

(A) .
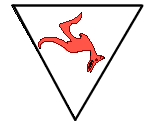(B) .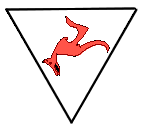
(C) .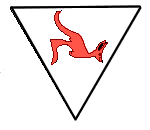
(D) .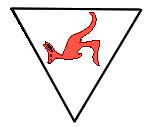
(E) .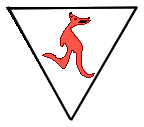


24 . Monica deve scegliere 5 numeri diversi in modo che, se ne moltiplica alcuni per 2 e gli altri per 3, i risultati diversi che ottiene siano nel minor numero possibile.
Qual è questo numero?
(A) 1.
(B) 2.
(C) 3.
(D) 4.
(E) 5.


25 . Un videogioco inizia con otto canguri messi in fila come mostra la figura:

A ogni mossa, Angelo può scambiare di posto due canguri vicini, ma solo se questi due canguri si guardano in faccia.
Il gioco prosegue fino a quando Angelo non può fare altri scambi.
Quante mosse farà Angelo?
 
(A) 2.
(B) 10.
(C) 12.
(D) 13.
(E) 16.


26 . Un sacchetto contiene solo gettoni rossi e gettoni blu.
In qualunque modo estraiamo 5 gettoni almeno uno è rosso; in qualunque modo ne estraiamo 6 almeno uno è blu.
Qual è il massimo numero di gettoni che possono essere contenuti nel sacchetto?
(A) 11.
(B) 10.
(C) 9.
(D) 8.
(E) 7.


27 . Il pavimento quadrato in figura 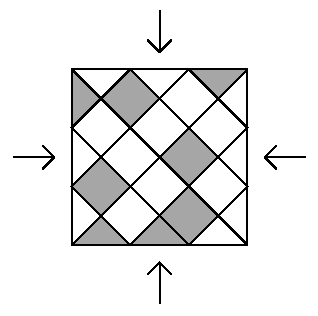è coperto con piastrelle triangolari e quadrate, alcune grigie, altre bianche.
Qual è il minimo numero di piastrelle grigie che è suficiente scambiare di posto con piastrelle bianche se vogliamo che la decorazione appaia uguale da ciascuna delle quattro direzioni evidenziate?
(A) Una triangolare, una quadrata.
(B) Una triangolare, tre quadrate.
(C) Tre triangolari, una quadrata.
(D) Tre triangolari, tre quadrate.
(E) Tre triangolari, due quadrate.


28 . Alice ama i numeri pari, Bianca ama i numeri divisibili per 3, Clelia ama i numeri divisibili per 5.
Un cestino contiene 8 biglie su ciascuna delle quali è scritto un numero: ognuna delle tre ragazze vi passa davanti in tempi diversi e, tra le biglie ancora presenti, prende tutte quelle con i numeri che ama.
Alla fine Alice ha collezionato le biglie con i numeri 32 e 52, Bianca quelle con i numeri 24, 33 e 45 e Clelia quelle con i numeri 20, 25 e 35.
In quale ordine le tre ragazze sono passate dal cestino?
(A) Alice, Clelia, Bianca.
(B) Clelia, Bianca, Alice.
(C) ) Bianca, Alice, Clelia.
(D) Bianca, Clelia, Alice .
(E) Clelia, Alice, Bianca.


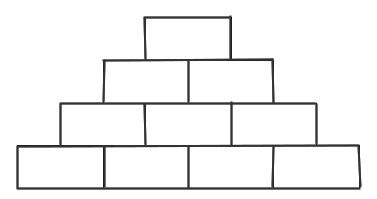
29 . Sara vuole scrivere un numero intero positivo in ogni casella del disegno in modo che ogni numero al di sopra della riga inferiore sia la somma dei due numeri nelle caselle immediatamente sotto a esso.


Quanti numeri dispari può scrivere al massimo Sara?
(A) 4.
(B) 5.
(C) 6.
(D) 7.
(E) 8.


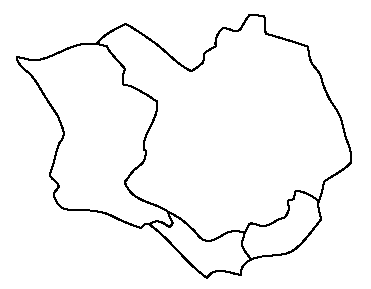
30 . Giulia ha quattro matite di colori diversi e vuole usarle (tutte o una parte) per colorare la mappa di un’isola divisa in quattro regioni, come mostra la figura.


Non vuole che due regioni coninanti abbiano lo stesso colore.
In quanti modi può colorare la mappa dell’isola?
(A) 12.
(B) 18.
(C) 24.
(D) 36.
(E) 48.